题目描述#

小 L 计划进行 $n$ 场游戏，每场游戏使用一张地图，小 L 会选择一辆车在该地图上完成游戏。

小 L 的赛车有三辆，分别用大写字母 $A$、$B$、$C$ 表示。地图一共有四种，分别用小写字母 $x$、$a$、$b$、$c$ 表示。

其中，赛车 $A$ 不适合在地图 $a$ 上使用，赛车 $B$ 不适合在地图 $b$ 上使用，赛车 $C$ 不适合在地图 $c$ 上使用，而地图 $x$ 则适合所有赛车参加。

适合所有赛车参加的地图并不多见，最多只会有 $d$ 张。

$n$ 场游戏的地图可以用一个小写字母组成的字符串描述。例如：$S=\texttt{xaabxcbc}$ 表示小L计划进行 $8$ 场游戏，其中第 $1$ 场和第 $5$ 场的地图类型是 $x$，适合所有赛车，第 $2$场和第 $3$ 场的地图是 $a$，不适合赛车 $A$，第 $4$ 场和第 $7$ 场的地图是 $b$，不适合赛车 $B$，第 $6$ 场和第 $8$ 场的地图是 $c$，不适合赛车 $C$。

小 L 对游戏有一些特殊的要求，这些要求可以用四元组 $(i, h_i, j, h_j)$ 来描述，表示若在第 $i$ 场使用型号为 $h_i$ 的车子，则第 $j$ 场游戏要使用型号为 $h_j$ 的车子。

你能帮小 L 选择每场游戏使用的赛车吗？如果有多种方案，输出任意一种方案。

如果无解，输出 -1。

输入格式#

输入第一行包含两个非负整数 $n$, $d$。

输入第二行为一个字符串 $S$。

$n$, $d$, $S$ 的含义见题目描述，其中 $S$ 包含 $n$ 个字符，且其中恰好 $d$ 个为小写字母 $x$。

输入第三行为一个正整数 $m$ ，表示有 $m$ 条用车规则。

接下来 $m$ 行，每行包含一个四元组 $i,h_i,j,h_j$ ，其中 $i,j$ 为整数，$h_i,h_j$ 为字符 $A$ 、$B$ 或 $C$，含义见题目描述。

输出格式#

输出一行。

若无解输出 -1。

样例#

样例输入#

3 1
xcc
1
1 A 2 B

样例输出#

ABA

小 $L$ 计划进行 $3$ 场游戏，其中第 $1$ 场的地图类型是 $x$，适合所有赛车，第 $2$ 场和第 $3$ 场的地图是 $c$，不适合赛车 $C$。

小 $L$ 希望：若第 $1$ 场游戏使用赛车 $A$，则第 $2$ 场游戏使用赛车 $B$。

那么为这 $3$ 场游戏分别安排赛车 $A$、$B$、$A$ 可以满足所有条件。

若依次为 $3$ 场游戏安排赛车为 $BBB$ 或 $BAA$ 时，也可以满足所有条件，也被视为正确答案。

但依次安排赛车为 $AAB$ 或 $ABC$ 时，因为不能满足所有条件，所以不被视为正确答案。

数据范围与提示#

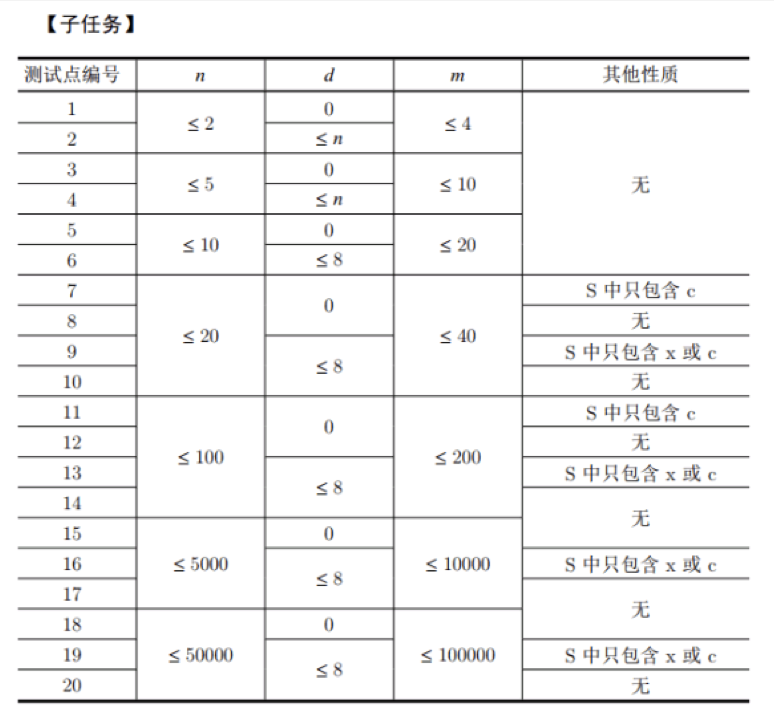
题解#

2-SAT

上来看这到题。
感到 $a,b,c$ 的时候很好搞， 但是不知道 $x$ 怎么办。
$a, b, c$ 的时候是2-SAT， 那 $x$ 不就是 3-SAT 了么。
这是NPC问题啊。

之后看来一下数据范围， $x \le 8$ 发现 $x$ 可以枚举。 然后就是一个裸的2-SAT了。

2-SAT 输出方案#

Tarjan

Tarjan缩点时会给联通块编号

对于一对相互对立的问题，谁的新编号小就选谁。

简单清真， 不用去跑什么 反图+拓扑排序 了。

#pragma GCC optimize("O3")
#include <bits/stdc++.h>
using namespace std;
inline int read() {
  int x = 0, f = 1;
  char ch = getchar();
  while (ch < '0' || ch > '9') {
    if (ch == '-') f = -1;
    ch = getchar();
  }
  while (ch >= '0' && ch <= '9') {
    x = x * 10 + ch - '0';
    ch = getchar();
  }
  return x * f;
}
const int MAXN = 50005;
const int MAXM = 100005;
struct data {
  int i, hi, j, hj;
} D[MAXM];
struct edge {
  int END, next;
} v[MAXM << 2];
int first[MAXN << 1], p;
void add(int a, int b) {
  v[p].END = b;
  v[p].next = first[a];
  first[a] = p++;
}
char tmp[2][5];
char S[MAXN];
int id[10];
int ID(int x, int y) {
  if (S[x] - 'a' == y) return 0;
  if (S[x] == 'a') return x * 2 + y - 1;
  else if (S[x] == 'b') return x * 2 + y / 2;
  else return x * 2 + y;
}
int dfn[MAXN << 1], low[MAXN << 1], Index, belong[MAXN << 1], T;
bool vis[MAXN << 1];
int st[MAXN << 1], top;
void Tarjan(int rt) {
  dfn[rt] = low[rt] = ++Index;
  st[++top] = rt;
  vis[rt] = 1;
  for (int i = first[rt]; i != -1; i = v[i].next) {
    if (!dfn[v[i].END]) {
      Tarjan(v[i].END);
      low[rt] = min(low[rt], low[v[i].END]);
    } else if (vis[v[i].END])
      low[rt] = min(low[rt], dfn[v[i].END]);
  }
  if (low[rt] == dfn[rt]) {
    T++;
    int x;
    do {
      x = st[top--];
      vis[x] = 0;
      belong[x] = T;
    } while (low[x] != dfn[x]);
  }
}
bool Calc(int n, int m) {
  memset(first, -1, sizeof(first)), p = 0;
  memset(dfn, 0, sizeof(dfn));
  memset(low, 0, sizeof(low));
  memset(belong, 0, sizeof(belong));
  T = Index = 0;
  for (int i = 1; i <= m; ++i) {
    int t1 = ID(D[i].i, D[i].hi);
    int t2 = ID(D[i].j, D[i].hj);
    if (t1) {
      if (t2) add(t1, t2), add(t2 ^ 1, t1 ^ 1);
      else add(t1, t1 ^ 1);
    }
  }
  for (int i = 2; i <= 2 * n + 1; ++i) {
    if (!dfn[i]) Tarjan(i);
    if (i & 1) {
      if (belong[i] == belong[i - 1]) return 0;
    }
  }
  for (int i = 1; i <= n; ++i) {
    if (belong[2 * i] < belong[2 * i + 1]) {
      if (S[i] == 'a') printf("B");
      if (S[i] == 'b') printf("A");
      if (S[i] == 'c') printf("A");
    } else {
      if (S[i] == 'a') printf("C");
      if (S[i] == 'b') printf("C");
      if (S[i] == 'c') printf("B");
    }
  }
  printf("\n");
  return 1;
}
int main() {
  int n = read(), d = read();
  scanf("%s", S + 1);
  int x = 0;
  int m = read();
  for (int i = 1; i <= m; ++i) {
    scanf("%d%s%d%s", &D[i].i, tmp[0], &D[i].j, tmp[1]);
    D[i].hi = tmp[0][0] - 'A';
    D[i].hj = tmp[1][0] - 'A';
  }
  for (int i = 1; i <= n; ++i)
    if (S[i] == 'x') id[++x] = i;
  int N = (1 << d) + 1;
  for (int i = 0; i <= N; ++i) {
    for (int j = 1; j <= x; ++j)
      if (i & (1 << (j - 1))) S[id[j]] = 'a';
      else S[id[j]] = 'b';
    if (Calc(n, m)) return 0;
  }
  return printf("-1\n"), 0;
}